10. Area and Average Value

b1. Area Between Two Curves

Here is a slight generalization of the area below a curve:

Find the area below a function \(y=f(x)\) above a function \(y=g(x)\) between \(x=a\) and \(x=b\).

We mimic what we did for the area under a curve.

We again divide the region into \(n\) rectangles each of width \(\Delta x=\dfrac{b-a}{n}\) but this time the height is \(f(x_i^*)-g(x_i^*)\) where \(x_i^*\) is a point in the \(i^\text{th}\) interval.

The area is then obtained by adding up the areas of the rectangles and taking the limit as the number of rectangles becomes large, (\(n\rightarrow\infty\)): \[ A=\lim_{n\rightarrow\infty}\sum_{i=1}^n [f(x_i^*)-g(x_i^*)]\Delta x \] This limit of a sum is recognized as the integral \[ A=\int_a^b [f(x)-g(x)]\,dx \]

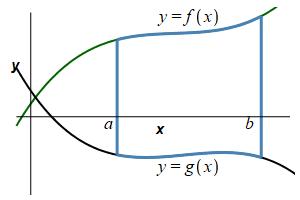
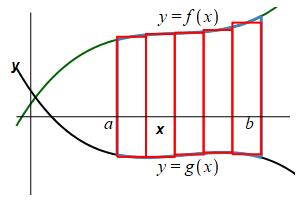
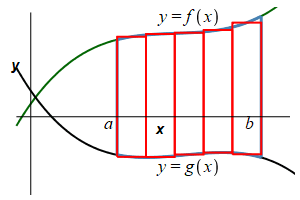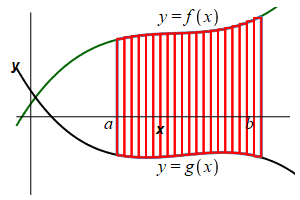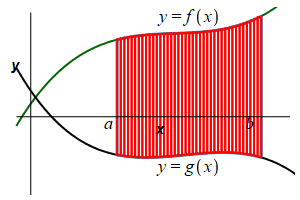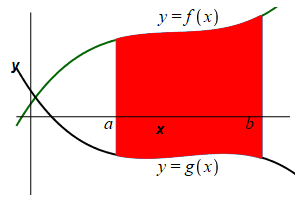
The area below a function \(y=f(x)\) above a function \(y=g(x)\) between \(x=a\) and \(x=b\) is: \[ A=\int_a^b [f(x)-g(x)]\,dx \]

Plot the parabolas \(y=x^2-2x\) and \(y=-x^2+4x\) and find the area between them.

To graph the two parabolas, we note that the \(x\)-intercepts are \(0\) and \(2\) for the first parabola and \(0\) and \(4\) for the second parabola. To find where they intersect, we equate the functions and solve: \[\begin{aligned} x^2-2x&=-x^2+4x \\ 2x^2-6x&=0 \\ x&=0,3 \end{aligned}\] Then the area is

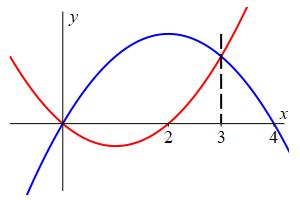
\[\begin{aligned} A&=\int_0^3 \text{upper}-\text{lower}\,dx \\ &=\int_0^3 (-x^2+4x)-(x^2-2x)\,dx \\ &=\int_0^3 (-2x^2+6x)\,dx =\left[-2\dfrac{x^3}{3}+3x^2\right]_0^3=9 \end{aligned}\]

How do you know which is upper and which is lower?

The parabola \(y=-x^2+4x\) bends down because of the minus before the \(x^2\). So it is on top.

Now you try:

Plot the parabola \(y=x^2-4\) and the line \(y=3x\) and find the area between them.

To find the intersection points, we equate the functions: \[x^2-4=3x\]

\(\displaystyle A=\int_{-1}^4 [3x-(x^2-4)]\,dx=\dfrac{125}{6}\)

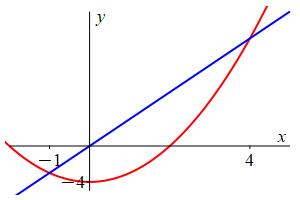
The parabola has \(y\)-intercept \(-4\) and opens up. The line passes thru the origin with positive slope. To find the intersection points, we equate the functions \[\begin{aligned} x^2-4&=3x \\ x^2-3x-4&=0 \\ (x-4)(x+1)&=0 \\ x&=-1,4 \end{aligned}\] So the area is

\[\begin{aligned} A &=\int_{-1}^4 [3x-(x^2-4)]\,dx \\ &=\int_{-1}^4 (3x-x^2+4)\,dx =\left[\dfrac{3x^2}{2}-\dfrac{x^3}{3}+4x\right]_{-1}^4 \\ &=\left(24-\dfrac{64}{3}+16\right) -\left(\dfrac{3}{2}+\dfrac{1}{3}-4\right) =\dfrac{125}{6} \end{aligned}\]

You can practice computing Areas between Curves by using the following Maplet (requires Maple on the computer where this is executed):

Area of a Region Rate It

For now, just look at the problems where \(y\) is a function of \(x\).

10. Area and Average Value

b1. Area Between Two Curves

How do you know which is upper and which is lower?

Heading